フォーカルπシェイパー9_HP

高出力ps/fsレーザー用に、ガウシアンビームを、フラットトップ/トップハット、ドーナツスポットに変換する、フォーカスレーザービーム用の高効率ビームシェイパーです。
紫外, 可視光, 近赤外, 中赤外にご使用頂けます。
データシートはこちら>> f_pishaper_9_leaflet
フォーカルπシェイパーを使用することで、集光スポットの強度分布を柔軟に操作することが可能になります。ほぼ100%の効率でフォーカルπシェイパーは微細加工に最適な集光スポットを作り出します。
基本的な操作原理
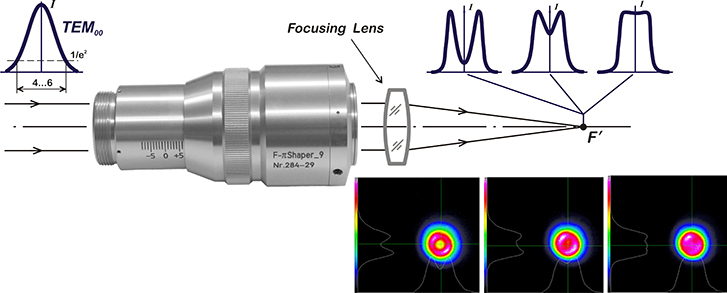
Focal-πShaperは、ガウス分布などのシングルモード レーザービームの強度分布を、フラットトップ/トップハット、逆ガウス、ドーナツなどの集光によるエアリーディスク分布のビームに変換する望遠鏡の光学系です。
- 同一デバイスでプロファイルを自在に操ることができる
- 最適な入力ビームサイズではサイドローブが発生しない
- ガウシアンビームの最適な2ω径は4…6 mm (1/e²)
- ミスアライメントやビームサイズの変化に対する感度が低い
- 広いスペクトルバンド
- 内部集光のない光学設計
- 回折限界のある集光レンズを適用可能
- ミラースキャナー、ポリゴンスキャナー、F-Θレンズなどのスキャニング光学系に最適
主なアプリケーション
・3Dプリンティング(選択的レーザー融解)
・微細加工
・穴あけ加工
・スクライビング
・切断
・マイクロ溶接
・太陽電池の加工技術
・地球物理学研究におけるレーザー加熱
仕様
| 一般的なπシェイパー9_HPモデル |
| タイプ |
ガリレオタイプの望遠鏡 (内焦点なし) |
| 入力ビーム |
シングルモード, コリメートまたは低発散/収束、
±5mradの範囲の全発散角 |
| フルサイズの直径 < 16 mm |
| ガウスビームの最適な2ω径 5…6 mm (1/e²) |
| 出力ビーム |
コリメートまたは低発散/収束 |
回折制限レンズの焦点領域における
スポット強度分布の操作に最適化 |
| フルサイズの直径 < 16 mm |
フォーカス
スポット |
ラウンドシェイプ |
| 可変プロファイル:フラットトップ/トップハット、逆ガウス、ドーナツ |
| 透過率 |
> 97%以上が使用可能なスペクトル帯域 |
その他
特徴 |
機器への組み込みが容易 |
| 科学・工業用途に適したコンパクトデザイン |
| 様々なタイプの回折限界集束レンズで動作 |
| アライメントが容易 |
| レンズとの距離は20~500mmの範囲で自由に設定可能* |
| 走査光学系に最適化:ミラースキャナー、ポリゴンスキャナー、F-Θレンズ |
| 外形寸法 |
直径:44mm (_1064_HPは39mm) |
| 長さ:93mm (_1064_HPは104mm) |
| マウント |
外側:M27x1スレッド@入口 |
| 質量 |
< 220g |
*その他の距離につきまてしもご相談ください。
| #型番 |
最適スペクトル (nm) |
設計波長 (nm) |
ベース アプリケーション |
| _1940_HP |
1850 – 2050 |
1940 |
mid-IR |
| _1550_HP |
1450 – 1650 |
1550 |
near-IR |
| _1064_HP |
1020 – 1100 |
1064 |
Nd:YAG, Fiber,
その他near-IR |
| _TiS_HP |
750 – 850 |
800 |
Ti:Sapphire, near-IR |
| _532_HP |
510 – 550 |
532 |
第2高調波 Nd:YAG,
類似のレーザー |
| _355_HP |
340 – 370 |
355 |
第3高調波 Nd:YAG,
類似のレーザー |
| _266_HP |
255 – 275 |
266 |
第4高調波 Nd:YAG,
類似のレーザー |
データシートはこちら>> f_pishaper_9_leaflet
1. スクライビング (提供: AoPhANOV)
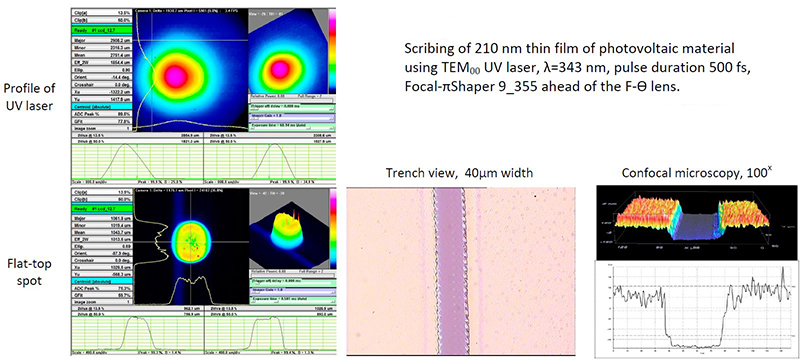
シングルモードUVレーザー、λ=343nm、パルス幅500fs、Fθレンズ前方にFocal πShaper 9_355を用いて、太陽電池材料の210nmの薄膜をスクライビング。
2. DACのレーザー加熱、地球物理学 (提供: シカゴ大学CARS)
タングステン箔の加熱の比較:
・(左列)レンズで集光したシングルモード ビーム
・(右列)前方にFocal-πShaperを設置したレンズで集光したシングルモード ビーム
トップダウンで段階的にパワーを上げていく。
ドットの明るさは温度に対応する。
Focal-πShaperを用いたシングルモード ビームでは、温度(明るさ)の変化のみで
ビーム径がほぼ一定であることがわかる。

お見積・お問合せはコチラ>>
フォーカルπシェイパーNA0.1 / NA0.06

高出力シングルモードファイバーレーザーのガウシアンからフラットトップ/トップハットに変換。
Focal-π Shaperは、ほぼ100%の高効率で様々なプロファイルを生成します。
・フラットトップ/トップハット
・逆ガウス
・ドーナツ
データシートはこちら>>f_pishaper_na_leaflet
主なアプリケーション
・微細加工、材料微細加工
・穴空け
・レーザー溶融
・レーザー加熱による地球物理学研究
・マーキング、彫刻
・スクライビング
・カット、印刷
仕様
| タイプ |
コリメーター(内部焦点無し) |
| 入力ビーム |
– シングルモード, M² < 1.4
– 広がり |
| 出力ビーム |
– コリメートまたは低広がり
– 回折限界集光レンズの焦点付近の強度分布を操作するために最適化
– 直径 < 20 mm |
| スペクトル範囲 |
1020 – 1100 nm |
| レーザー出力 |
2 kWまで (CW) |
| その他の特長 |
– 水冷
– ファイバーレーザー運用に適応
– QBHコネクタ対応
– 工業アプリケーションに適したコンパクトな設計
– あらゆるタイプの回折限界集光レンズで動作
– 簡単調整
– スキャン光学系に最適化:ミラースキャナー、F-θレンズ |
| 全体寸法 |
– 直径: 77 mm
– 長さ: 130 mm |
| マウント |
入力 (ファイバー側): 内部ネジM 30×0.75, 5軸QBHマウント
出力: 外ネジ M 30×0.75 |
| 重さ |
650 g |
| モデル |
Focal-πShaper NA0.1 50_80_1064 |
Focal-πShaper NA0.06 50_80_1064 |
入力広がり角
2Θ (1/e²), rad |
0.2 – 0.24 |
0.1 – 0.12 |
 お見積・お問合せはコチラ>>
お見積・お問合せはコチラ>>
フォーカルπシェイパー12_CO2
※このシリーズは製造終了になりました。

CO2レーザーのシングルモード集光ビームの強度プロファイルを操作。
Focal-πShaperはほぼ100%の効率で様々なプロファイルを生成します。
・フラットトップ/トップハット
・逆ガウス
・ドーナツ
・トライデントなど
データシートはこちら>> f_pishaper_12_co2_leaflet
主なアプリケーション
- マーキングと彫刻
- 穴あけ加工
- スクライビング
- ダイシング
- 印刷
- 溶接
仕様
| タイプ |
ガリレオ型望遠鏡(内部焦点無し) |
| 入力ビーム |
-シングルモード、全発散角±5mradのコリメートまたは低発散 |
| -直径<24mm |
| -ガウシアンビームの最適な2ω径 8〜12 mm (1/e²) |
| 出力ビーム |
-コリメートまたは低発散 |
| -回折限界レンズの焦点面におけるフラットトップ/トップハット、ドーナツスポットに最適化 |
| -直径<24mm |
| その他特徴 |
-機器への容易な取付 |
| -科学、産業用に適したコンパクトなデザイン |
| -あらゆるタイプの回折限界集光レンズで動作 |
| -簡単調整 |
| -走査光学系に最適化:ミラースキャナー、F-θレンズ |
| 全体寸法 |
-直径 48mm
-長さ <139mm |
| マウント |
外ネジ M 27×1 |
| 重さ |
400g |
| 型番 |
Focal-πShaper 12_CO2_10.6
|
Focal-πShaper 12_CO2_9.4
|
| スペクトル範囲 |
10.5 – 10.7μm |
9.3 – 9.5μm |
※Focal-πShaper 12_CO2シリーズ 後継機種
Focal-πShaper 12_CO2_10.6 →Focal-πShaper 10_CO2_10.6
Focal-πShaper 12_CO2_9.4 →Focal-πShaper 10_CO2_9.4 または Focal-πShaper CO2_Q-10
お見積・お問合せはコチラ>>
フォーカルπシェイパー10_CO2

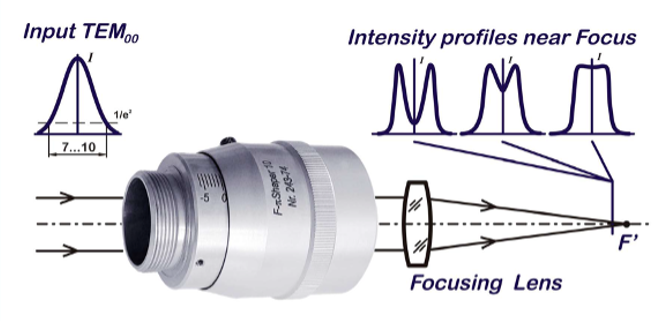
CO2レーザーのTEM00集光用高効率ビームシェイパーシリーズ
集光スポットの強度分布を自在に操作。
ほぼ100%の効率とサイドローブなしで、フォーカルシェイパーは微細加工で最適なものを作り出します。
主なアプリケーション
- 切断
- スクライビング
- マーキングと彫刻
- 穴あけ
- 材料の微細加工
- 印刷
- マイクロ溶接
仕様
|
Common for all Focal Shaper 10_CO2 models:
|
|
Type
|
Telescope of Galilean type ( without internal focus)
|
|
Input beam
|
– TEM00, Collimated or low divergent with full divergence angle ±5 mrad
– Diameter < 20 mm
– Optimum 2 diameter for a Gaussian beam 7…10mm (1/e2)
|
|
Output beam
|
– Collimated or low divergence
– Profile is optimized for flat top, doughnut spot in focal plane of a diffraction limited lens
– Diameter < 15 mm
|
|
Other features
|
– Easy integration in equipment
– Compact design suitable for scientific and industrial applications
– Operation with diffraction limited focusing lens of any type
– Easy alignment
– Optimized to work with scanning optics: mirror scanners, F theta lenses
|
|
Overall dimensions
|
– Diameter 45 mm
– Length <72 mm
|
|
Weight
|
250 g
|
|
Mounting
|
External Thread M 27×1
|
|
Focal Shaper 12_
CO2 features
|
|
|
|
Model
|
F-πShaper 10_CO2 _10.6
|
F-πShaper 10_CO2 _9.4
|
|
Optimum spectral
range**
|
10.2 – 10.9μm
|
9.1 – 9.7μm
|
|
* working wavelength range without taking into consideration the coatings
** according to coatings applied
|
データシートはこちら>>Focal-piShaper_10_CO2.pdf
フォーカルπシェイパー Q

ガウシアンをフラップトップ、またはドーナツ型に変換する集光スポット用高効率レーザービームシェイパー。フラットトップ/トップハットやドーナツ型の集光スポットを得るため、エアリーディスク型に変換します。
データシートはこちら>> f_pishaper_q_leaflet
主なアプリケーション
・3Dプリント—パウダーベッド方式
・微細加工、穴あけ加工
・スクライビング
・マイクロ溶接
・太陽電池加工
・切削
仕様
| 共通仕様 |
| 入力ビーム |
-シングルモード、通常M2 < 1.5 |
| -広がり角±20 mrad以内 |
| 透過率 |
動作スペクトル範囲で >99% |
| アライメント |
X/Y 横方向移動、±2mmレンジ |
レイアウト例:シングルモードファイバーレーザーでのパウダーベッド方式
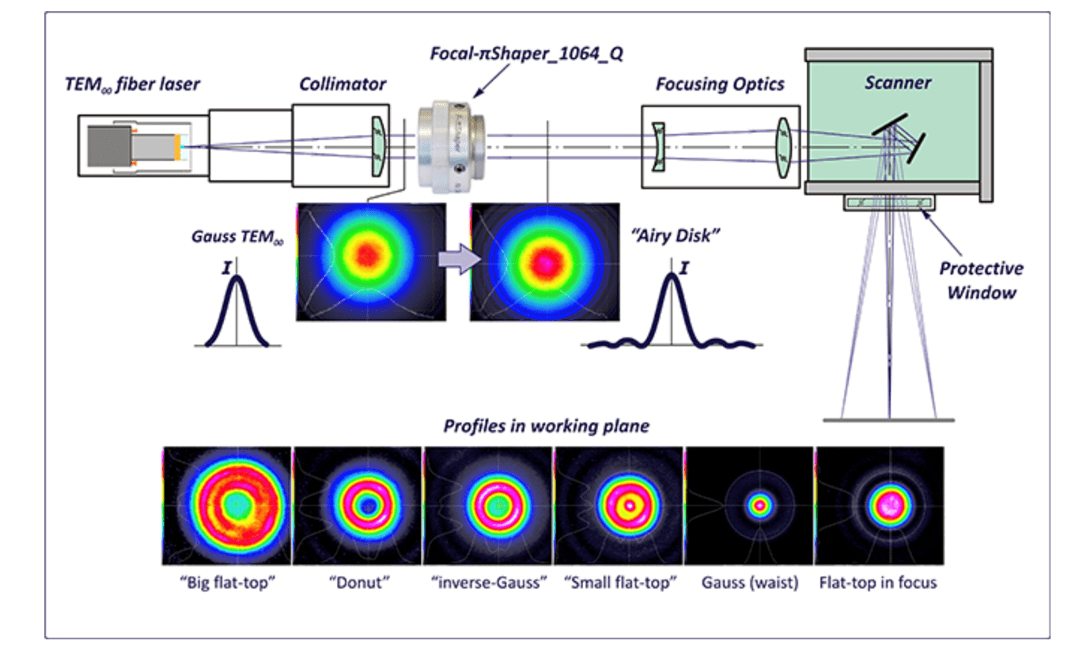
SLM過程による例

お見積・お問合せはコチラ>>
.


AdlOptica社はマルチフォーカスおよびレーザービーム成形光学の分野で活躍しているメーカーです。UVからIRまでのスペクトル、mWからkWまでの出力、CWまたはパルスレーザー、アクロマティックデザインなど、様々なアプリケーションに対応しております。
Adloptica社の製品一覧はこちら

















